在實作 Support Vector Machine 前，先簡介一下它可以做的任務類型。

支持向量機（Support Vector Machine，SVM）可以用於分類（classification），也可以用於回歸（regression）任務。

1. 分類（Classification）：
   SVM 在分類問題中是想尋找一個能夠將不同類別的數據點分隔開的最優超平面（最優分類器）。超平面是一個具有最大邊際（即兩個不同類別之間的最短距離）的決策邊界。SVM 通過最大化兩個不同類別之間的邊際來找到這個超平面。如果數據不是線性可分的，SVM 還可以使用內核技巧將數據映射到高維空間，使其在該空間中變得線性可分。

2. 回歸（Regression）：
   SVM 也可以應用於回歸問題，這種變種稱為支持向量機回歸（Support Vector Machine Regression，SVR）。在回歸中，SVM 的目標是擬合一個模型，以預測連續型目標變量，而不是類別。SVR 的目標是找到一條超平面，使實際數據點盡量靠近這個超平面，同時保持邊際內的點的誤差越小越好。通過調整模型的參數，可以控制邊際的大小以及模型的複雜度，以滿足特定的回歸任務需求。

Implementation

這裡我們會先用 PCA 作為數據預處理，它可以幫助我們用於數據的降維和特徵提取。

特別是當我們在使用要 SVM 的數據集具有高維度且存在冗餘特徵時。

通過使用 PCA 降低維度，可以減少SVM模型的計算複雜性，提高模型的訓練速度，並減少過度擬合的風險。

Import Library

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import svm # Only use SVC from sklearn

這裡的 sklearn 僅會在使用到 SVC 時被呼叫。

Load Dataset

data = pd.read_csv("./x_train.csv",header= None)/255
label = pd.read_csv("./t_train.csv",header= None)

路徑的部分需要依據資料集的路徑做更改。

Principal components analysis

data_new = data.values - np.mean(data.values, axis=0) # centralize data
np.allclose(data_new.mean(axis=0), np.zeros(data_new.shape[1])) # check if centralization is correct
C = (data_new.T @ data_new) / (data_new.shape[0] - 1) # covariance matrix
eig_vals, eig_vecs = np.linalg.eig(C) # eigenvalues and eigenvectors
eig_vals, eig_vecs = eig_vals.real, eig_vecs.real # convert to real numbers
# sort eigenvalues in ascending order   
eig_vals_sorted = np.argsort(eig_vals)[::1][-2:] # sort eigenvalues in ascending order and take the last two
data_pca = data_new @ eig_vecs[:,eig_vals_sorted] # PCA

以上是 Principal components analysis（PCA）的步驟，用於對數據進行降維。

data_new = data.values - np.mean(data.values, axis=0)

此步驟將數據矩陣 data 中的每一列數據減去該列的平均值，從而實現了數據的中心化（去中心化）。

中心化是PCA的必要步驟，它有助於將數據集的均值移動到原點，以便更好地進行特徵提取。

np.allclose(data_new.mean(axis=0), np.zeros(data_new.shape[1]))

用於確保數據已經被正確中心化，它檢查每一列的平均值是否接近零。

C = (data_new.T @ data_new) / (data_new.shape[0] - 1)

計算數據的協方差矩陣 C。協方差矩陣用於描述數據中不同特徵之間的關係，是PCA的核心計算。

eig_vals, eig_vecs = np.linalg.eig(C)

計算協方差矩陣的特徵值（eigenvalues）和特徵向量（eigenvectors）。

特徵值表示數據中主要變異性的量度，而特徵向量則是特徵空間中的方向，它們用於找到主成分。

eig_vals, eig_vecs = eig_vals.real, eig_vecs.real

將特徵值和特徵向量轉換為實數。

eig_vals_sorted = np.argsort(eig_vals)[::1][-2:]

排序特徵值並選擇最大的兩個特徵值（這是根據主成分的數量而定的選擇，通常是將數據降到二維）。

這些特徵值對應於數據中的主要變異性。

data_pca = data_new @ eig_vecs[:,eig_vals_sorted]

最後，使用選定的特徵向量對原始中心化數據進行投影，從而實現數據的降維。

data_pca 包含了降維後的數據，其中每一列代表一個主成分。

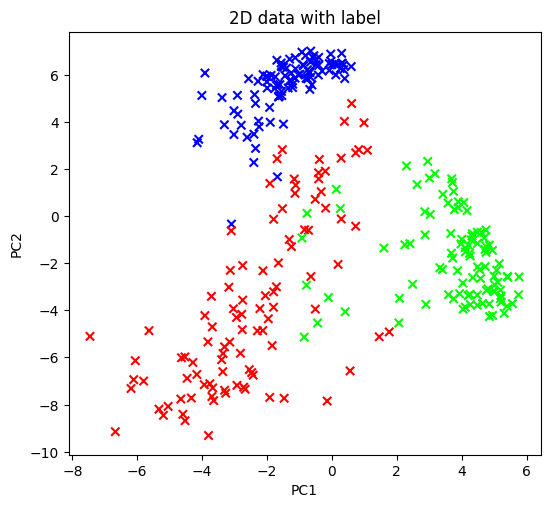
上圖是經過 PCA 轉換後的圖

Support Vector Machine from scratch

class SVM (object):
    def __init__(self, kernel='linear', C=1.0, gamma='auto'):
        self.kernel = kernel
        self.C = C
        self.gamma = gamma
        self.alpha = None
        self.b = None
        self.support_vector = None
        self.support_vector_label = None

    def _kernel(self, x1, x2):
        if self.kernel == 'linear':
            return x1 @ x2.T
        elif self.kernel == 'rbf':
            return np.exp(-self.gamma * np.linalg.norm(x1 - x2) ** 2) # gamma = 1 / (2 * sigma^2)
        elif self.kernel == 'poly':
            return (1 + x1 @ x2.T) ** self.gamma
        else:
            raise ValueError('kernel not supported')

    def fit(self, x, y):
        n_samples, n_features = x.shape
        K = np.zeros((n_samples, n_samples))
        for i in range(n_samples):
            for j in range(n_samples):
                K[i, j] = self._kernel(x[i], x[j])
                
        '''
        define and solve QP problem
        min 1/2 x^T P x + q^T x
        s.t.
        Gx <= h
        Ax = b
        x >= 0
        '''
        
        P = np.outer(y, y) * K # P = y^T y K
        q = -1 * np.ones(n_samples) # q = -1
        G = np.diag(np.ones(n_samples) * -1) # G = -I
        h = np.zeros(n_samples) # h = 0
        A = y.T # A = y^T
        b = np.zeros(1) # b = 0
        a = np.linalg.solve(np.dot(G, P) + np.eye(n_samples), np.dot(G, q)) # Lagrange multipliers

        sv = a > 1e-5 # support vectors
        ind = np.arange(len(a))[sv] # indices of support vectors
        self.alpha = a[sv] # Lagrange multipliers of support vectors
        self.support_vector = x[sv] # support vectors
        self.support_vector_label = y[sv] # labels of support vectors

        # Intercept
        # b = 1/n sum(y_n - sum(alpha_i y_i K(x_n, x_i)))
        self.b = 0
        for n in range(len(self.alpha)):
            self.b += self.support_vector_label[n]
            self.b -= np.sum(self.alpha * self.support_vector_label * K[ind[n], sv])
        self.b /= len(self.alpha)

        # Weight vector
        # w = sum(alpha_i y_i x_i)
        if self.kernel == 'linear':
            self.w = np.zeros(n_features)
            for n in range(len(self.alpha)):
                self.w += self.alpha[n] * self.support_vector_label[n] * self.support_vector[n]
        else:
            self.w = None

    def predict(self, x):
        if self.w is not None:
            return np.sign(x @ self.w + self.b)
        else:
            y_predict = np.zeros(len(x))
            for i in range(len(x)):
                s = 0
                for alpha, sv_y, sv in zip(self.alpha, self.support_vector_label, self.support_vector):
                    s += alpha * sv_y * self._kernel(x[i], sv)
                y_predict[i] = s
            return np.sign(y_predict + self.b)

    def score(self, x, y):
        y_predict = self.predict(x)
        return np.mean(y_predict == y)

上述是實作 Support Vector Machine 的程式碼

__init__(self, kernel, C, gamma)

初始化 SVM 類的實例，可以指定不同的核函數（linear、rbf、poly）、正則化參數 C，以及 gamma 參數。

_kernel(self, x1, x2)

計算不同 kernel function 下的內積或相似度。

Kernel function 包括

• Linear kernel
• Gaussian kernel (rbf)
• Polynomial kernel

fit(self, x, y)

用於訓練 SVM 模型，接受輸入特徵 x 和對應的標籤 y。

在此方法中，計算了核矩陣（K）並解決了二次規劃（QP）問題以獲得 support vector、label和 Lagrange 乘數。

同時計算了 bias（b）和 weight（w）。

predict(self, x)

用於對新數據進行預測。根據已經訓練好的模型，計算並返回預測類別的標籤。

score(self, x, y)

計算模型的預測精度，即預測標籤和實際標籤之間的匹配程度。

使用不同的 kernel function 來處理不同類型的數據，並支持調整正則化參數 C 和 kernel function 的參數。

透過 Lagrange 乘數的計算，以找到支持向量和相應的模型參數。

這裡使用 Support Vector Machine 進行分類任務，並通過訓練該模型並使用 predict 方法進行預測。

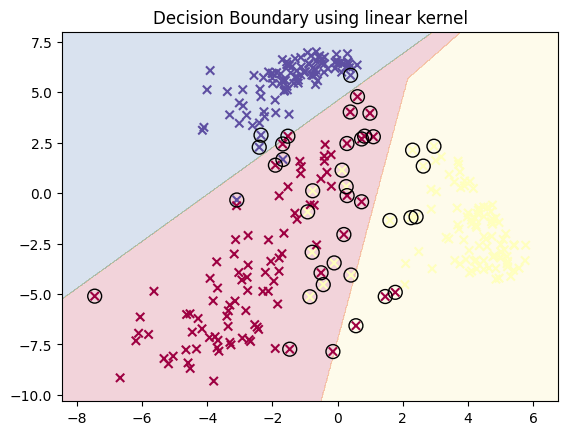
上圖就是透過 Kernel function 使用 Support Vector Machine 進行分類任務的結果。

詳細的內容可以觀看 Notebook

明天會透過 Kaggle competition 中的來演練 House Prices

在此也感謝關注我文章的各位。